Tech.eduidea.id – Huffman Code adalah salah satu metode dalam penyederhanaan suatu data, biasanya metode tersebut digunakan dalam proses kompresi data atau citra supaya size nya bisa lebih kecil

Contoh Penerapan Huffman Code

Misal terdapat suatu data memiliki ukuran 500KB, lalu size nya ingin diperkecil menjadi 300KB, nah, salah satu metode kompresi yang bisa digunakan adalah Metode Huffman Code. 

Salah satu metode Huffman code untuk melakukan kompresi atau penyerhanaan data adalah dengan menggunakan Huffman Tree.

Teorema dari Huffman Code adalah sebagai berikut: 
Jika p_j > p_i , maka, l_j ≤ l_i2.

Ket:
S = Sumber
P = Probabilitas
C = Codeword
l = Panjang

Dua Codeword dari dua simbol dengan probabilitas terendah mempunyai panjang yang sama sedangkan dua Codeword terpanjang identik kecuali pada digit terakhir

Contoh Soal Huffman Coding dan Penyelesaiannya

Dimisalkan pada sebuah kalimat terdapat huruf-huruf yang muncul, dengan banyaknya kemunculan adalah sebagai berikut:

Huruf	Frekuensi kemunculan
a	5
b	7
c	10
d	14
e	20

Cara mencari Huffman Code dijelaskan di bawah ini:

Di bawah ini terdapat contoh metode Huffman Tree atau disebut juga metode pengakaran, dimana kita akan membuat suatu pola pengakaran pada pohon. Langkah pembentukan pohon huffman adalah sebagai berikut:

Untuk membuat Huffman Code pertama kita harus mengurutkan data frekuensi kemunculan dari yang trekecil seperti tabel diatas, lalu kita jumlah kan setiap data secara berpasangan dari yang terkecil:

maka kita mulai dengan menjumlahkan a dan b

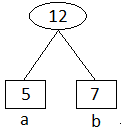
Maka tabel berubah menjadi sebagai berikut:

Huruf	Frekuensi
c	10
ab	12
d	14
e	20

Dari tabel di atas kita kembali jumlahkan dua nilai terkecil..c dan ab

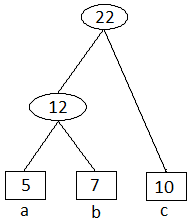
Maka tabel berubah menjadi sebagai berikut:

Huruf	Frekuensi
d	14
e	20
abc	22

Dari tabel di atas kita kembali jumlahkan dua nilai terkecil.. d dan e

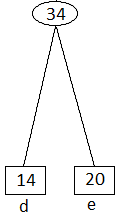
Maka tabel berubah menjadi sebagai berikut:

Huruf	Frekuensi
abc	22
de	34

Dari tabel di atas kita kembali jumlahkan dua nilai terkecil..abc dan de

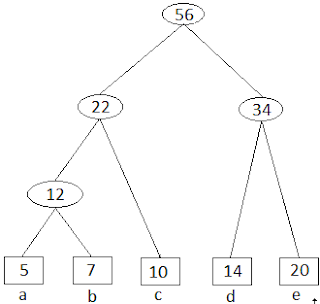
Lalu, karena semua Huruf telah dijumlahkan, kita  tambahkan angka 0 dikiri setiap cabang, dan angka 1 dikanan setiap cabang, seperti gambar di bawah ini:

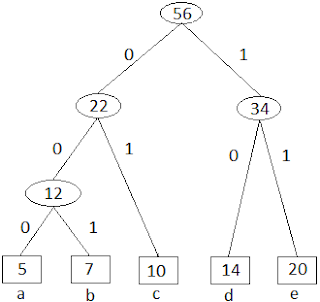
Dari data metode pengakaran Hufman tree di atas di dapatkan Codeword  untuk setiap huruf adalah sebagai berikut:

Huruf	CodeWord
a	000
b	100
c	10
d	01
e	11

Dari tabel diatas kita mendapatkan kode yang unik untuk setiap huruf dengan menggunakan Metoda Hufman Tree pada Hufman Code. 

Demikian contoh soal Huffman code dan cara penyelesaiannya menggunakan metode huffman tree.

Dengan kode-kode unik tersebut kita dapat menyederhanakan sebuah data dengan bahasa yang dipahami oleh komputer berupa angka binary (0 dan 1).

Contoh di atas adalah contoh sederhana tentang penyederhanaan sebuah data. Semakin beragam data yang tersedia semakin kompleks pula metode yang harus dilakukan untuk penyederhanaan sebuah data.

Jadi salah satu kegunaan dari Huffman code adalah untuk melakukan kompresi citra/data dengan algoritma Huffman code.